Hearing Involves Sound Physics

The way we hear sound is complex. The different attributes of sound (namely, intensity, frequency, the direction from which it is coming etc.) are faithfully perceived in the auditory cortex. The whole procedure may seem rather straightforward, but it is far more complicated than what looks so deceptively simple.

The sound waves (say from an orchestra) impinge on our eardrums. Sound waves are mechanical waves consisting of condensation and rarefaction, things we learned in our school days. These waves then vibrate our eardrums (Tympanic Membrane; TM). The TM is critically damped, meaning any vibration that is set in will stop almost instantaneously. The vibrating TM then transfers its mechanical energy to the oval window, in the membranous labyrinth of the cochlea, via an ossicular chain consisting of three (3) very small bones.

The membranous labyrinth consists of three adjoining tubes coiled side by side (as shown in the figure). If we were to make a section through it, we would find 3 separate compartments within it: Scala vestibuli, Scala media and Scala tympani. Scala vestibuli is connected to Scala tympani at the apex of the cochlea, a place called helicotrema. While Scala tympani contains a fluid called endolymph (a fluid rich in K+ or potassium ions); the other 2 tubes contain perilymph (a fluid very similar to plasma, rich in Na+ and low in K+). The sheer asymmetry in K+ distribution among the two adjacent fluids (endolymph and perilymph) generate an endocochlear potential of about +80mV, endolymph positive when the perilymph is considered as 0 (zero) volt or ground.

As the oval window vibrates, the fluid in Scala vestibuli (perilymph) also vibrates. Sound was traveling in air before it struck the eardrum, but here, we see that they are now propagating in a fluid medium, which has far more inertia than air. The possible impedance mismatch that would happen is compensated by the eardrum itself and the ossicular chain. The mechanical advantage of the lever system of the ossicular chain, together with the ratio of surface areas of TM and the 'oval window', amplifies the force of sound waves about 22 times, so that the total force at the oval window is 22 times than what the TM experienced originally.

Now, vibrations have set up in the Scala vestibuli form the oval window. These vibrations find their way to the Scala media, as the two tubes are separated by only a very thin membrane (Reissner’s membrane). Hence, fluid in the Scala media (endolymph) vibrates whenever the oval window is vibrating. This Youtube video beautifully illustrates it.



The vibrating endolymph sets up a wavy motion in the basilar membrane (BM). The ‘real analysis’ of sound waves starts here! The BM performs real time spectral analysis of sounds it is presented with (analysis of frequencies below 200Hz is skipped though). We normally hear in the frequency range of 20Hz to 20 kHz.

The hair cells in the organ of Corti, our hearing apparatus, are arranged in such a manner along the BM that those near the base of the cochlea will respond to high frequencies; while as we go up to the apex of the cochlea, the BM reacts best at low frequencies. In other words, each part of the BM has its own unique maxima, the frequency at which the BM responds most well. Below 200Hz, there is no such place encoding.


Our ears follow another principle. The ‘traveling wave’ spreads quicker near the base of the cochlea and its speed diminishes fast as it goes up. This ensures that a longer stretch is available for the higher frequencies; else the higher frequency part would have been bunched together, creating a loss in the HF range. This non linearity in traveling wave propagation is thus needed.

Generator Potential
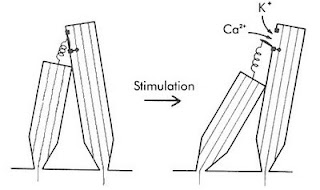The genesis of generator potentials in the hair cells is also interesting. Imagine that a group of persons of varying height are standing on a carpet. A thread is attached from the top button (of his shirt) of the smaller person to the top button of his taller counterpart. If the carpet is now tilted by pulling it up from the short person’s end, the thread will now be stretched snapping the taller person’s button. The hair cells also have threads (Tip Links) extending from shorter to their taller cousins. A traveling wave will cause pulling of tip links, resulting in the opening of a mechanically sensitive cation channel. Since potassium is the predominant cation in the endolymph, K+ will then enter the taller hair cells. Look at the electrical gradient around the hair cell; it is -140mV with respect to the endolymph (it is about negative 60 mV wrt the perilymph). So, cations, specially K+ rushes in  creating depolarization. A cascade of events like opening of voltage-gated Ca++ ion channels at the base, consequent fusion and exocytosis of vesicles discharging neurotransmitters, probably glutamate to the afferent cochlear nerve endings surrounding the hair cells, creating an action potential in the nerve.

Frequency Discrimination
When we listen to music, our ears pick up the frequencies in a number of ways. Firstly, the place (maxima) on the BM where maximum excitation takes place is actually a function of frequency. As a matter of fact, there is a frequency map along the BM. Secondly, at frequencies below 3 kHz, the nerves fire in synchrony with the incident sound waves. This is called the ‘volley principle’. The ‘phase locking’ of the two frequencies that occurs below 3 kHz, is highly analogous to the ‘phase locked loops’ in electronic circuits (NE565). Thus ‘volley principle’ allow us to discriminate frequencies. Actually, volley effect is more important in ‘loudness’ assessment. ‘Pitch’ (the subjective/psychological dimension related to frequency) are also moderated by factors such as loudness and the duration of sound. At low frequency (below 500 Hz) pitch seems lower and at higher frequencies (above 4 kHz) pitch seems higher, as the loudness increase, when the frequency is kept constant. Again, when the duration of sound increase from 0.01 second to 0.1 second, the pitch will rise too, for a particular frequency. Sound of less than 0.01 sec duration does not evoke appreciation of any pitch by us.

Loudness Discrimination
Loudness is the perceived intensity of sound, a subjective psychological dimension. The interpreted sound sensation is proportional to the cube root of the actual sound intensity. As such, the ear works at the top of its limit, at a point analogous to Hopf bifurcation, beyond which instability in oscillations occur.
As the sounds become louder, the amplitude of BM movement is more, resulting in more excitation of hair cells. Secondly, with greater loudness, the hair cells around the ‘maxima’ fire too. This causes spatial summation. Thirdly, the outer hair cells are stimulated at loud sounds. The brain will automatically infer loudness levels when cells corresponding to the outer hair cells fire.

Locating Sounds
Then there is location of the direction of sound. We can locate whether the drums are on the left and the lead guitar is to the right. This is achieved by calculating which ear gets the sound first (time lag) and/ or which ear gets it louder (intensity). The time lag method works below 3 kHz; while intensity method works at higher frequencies.
Front/ back discrimination is done by the pinna (auricle) of our ears due to their particular shape.

Auditory nerve
It is interesting that each auditory nerve fiber has its own characteristic frequency, the frequency at which it responds most well. However, it is true only at low intensity. At higher intensities, this specificity is lost and they then respond to a wider spectrum of frequencies. The auditory nerve produces a flurry of action potentials, the frequency of which depends on the intensity of the sound stimuli, it is exposed to. This is very much similar to ‘voltage to frequency converter’ ICs (LM331 is one such VFC IC), where a change in voltage at the input of VFC will cause a change in frequency at the output.

The auditory nerve then goes to the: cochlear nucleus in the medulla to Superior olivary nucleus to Inferior colliculus (via lateral lemniscus) to Medial Geniculate Body (in the Thalamus) to end in Auditory cortex. Some fibers cross to the other side early in their course while others cross at other levels. Fibers from primary auditory area sends association fibers to different parts of the brain for language processing and other tasks.
The nerve synapses with higher order neurons in the above places, which then relay to the nerves upstream. Everywhere in its course, including the nuclei, there are clearcut ‘tonotopic maps’, representing definitive frequency layouts. There are also extensive crossing of nerve fibers to the opposite side. Before the fibers reach the auditory cortex, they connect to many reflex pathways vital to life. For example, they send branches to the reticular activating system which keeps us awake during the noisy hours.

The auditory cortex (Brodmann’s area 41) is the portion of the cerebral cortex in the superior temporal gyrus. Its anterior part is mainly concerned with low frequency and the posterior part tackles the higher frequencies. Thus area 41 also has its own tonotopic map. Secondary auditory cortex (auditory association area) is vital for the interpretation of sounds. A person, in whom Wernicke’s area (part of auditory association area) is damaged, will hear normally but will fail to understand its meaning, leading to aphasia.

The sheer complexity of the auditory circuitry is really mind-boggling: the logarithms (we hear in a log scale, not a linear one), cube functions, phase locking are only some of them. The range of sound intensity (from whisper to the roar of a jet plane) we hear is about 1 trillion fold; but surprisingly, the auditory nerve fibers have a much less dynamic range. Yet we hear the full range. It’s really amazing.


P. Martin (2001). Compressive nonlinearity in the hair bundle's active response to mechanical stimulation Proceedings of the National Academy of Sciences, 98 (25), 14386-14391 DOI: 10.1073/pnas.251530498

Last modified: Mar 10, 2014
Reference: Textbook of Medical Physiology, 17e, Guyton and Hall